算法学习-二叉树
二叉树基本概念: 7.1 二叉树 - Hello 算法 (hello-algo.com)
1. 二叉树基础
1.1 定义二叉树
// TreeNode 二叉树节点
type TreeNode struct {
Value any
Left *TreeNode
Right *TreeNode
}
// NewTreeNode 构建二叉树节点
func NewTreeNode(value any) *TreeNode {
return &TreeNode{
Value: value,
Left: nil,
Right: nil,
}
}1.2 初始化二叉树
初始化如图所示的一个二叉树

func TestNewTreeNode(t *testing.T) {
// 定义节点
node1 := NewTreeNode(1)
node2 := NewTreeNode(2)
node3 := NewTreeNode(3)
node4 := NewTreeNode(4)
node5 := NewTreeNode(5)
// 构建二叉树
node1.Left = node2
node1.Right = node3
node2.Left = node4
node2.Right = node5
}2. 二叉树种类
2.1 完美二叉树(满二叉树)
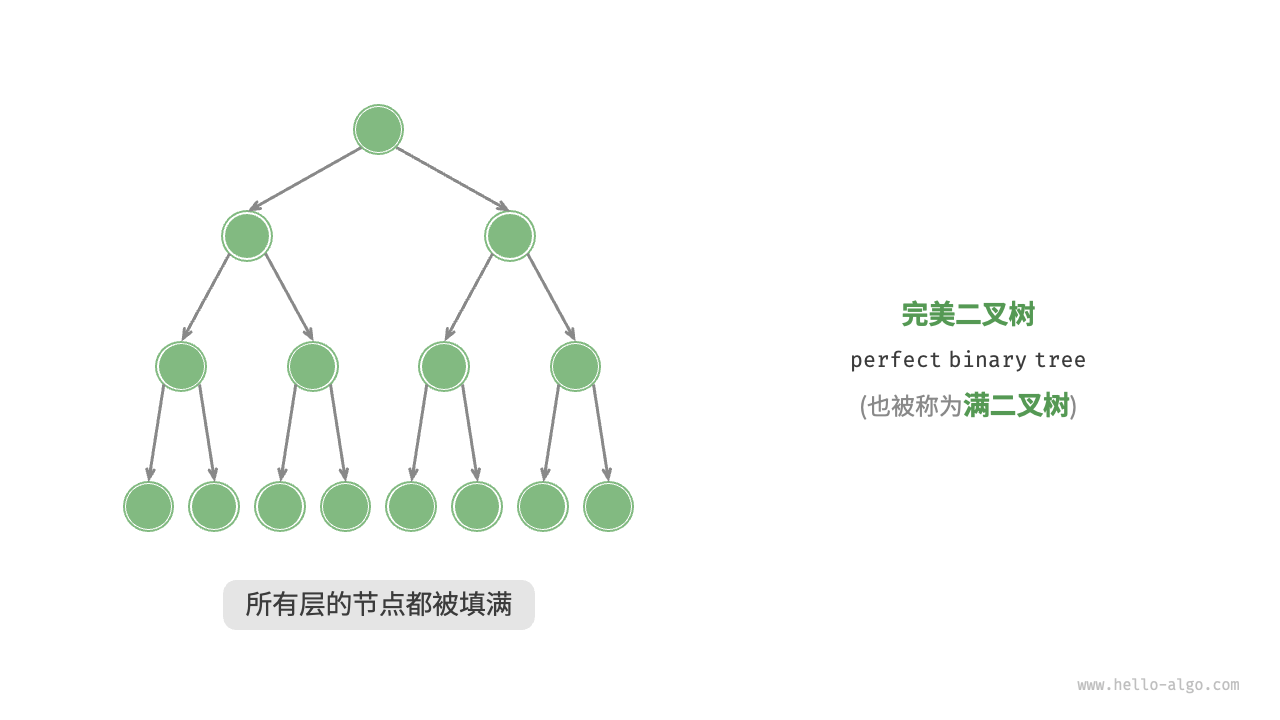
完美二叉树(perfect binary tree)所有层的节点都被完全填满。
在完美二叉树中,叶节点的度为 0 ,其余所有节点的度都为 2 ;若树的高度为 ℎ ,则节点总数为 2ℎ+1−1 ,
2.2 完全二叉树
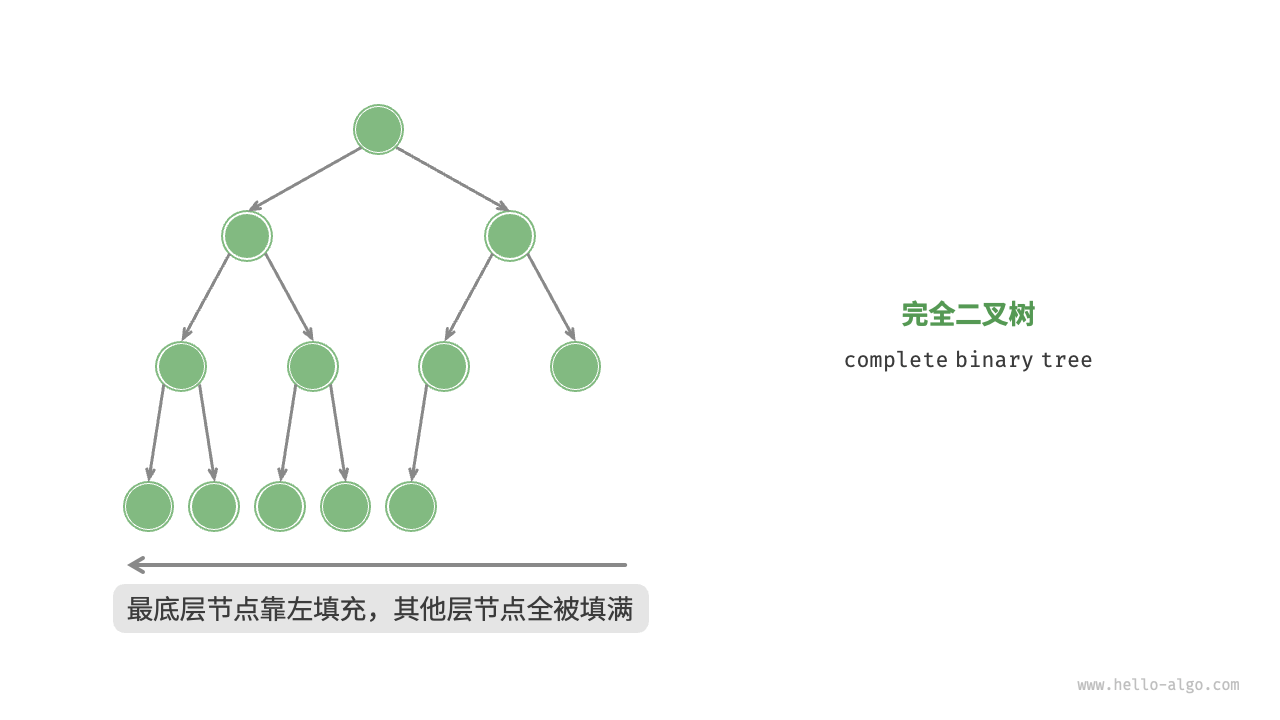
完全二叉树(complete binary tree)只有最底层的节点未被填满,且最底层节点尽量靠左填充。
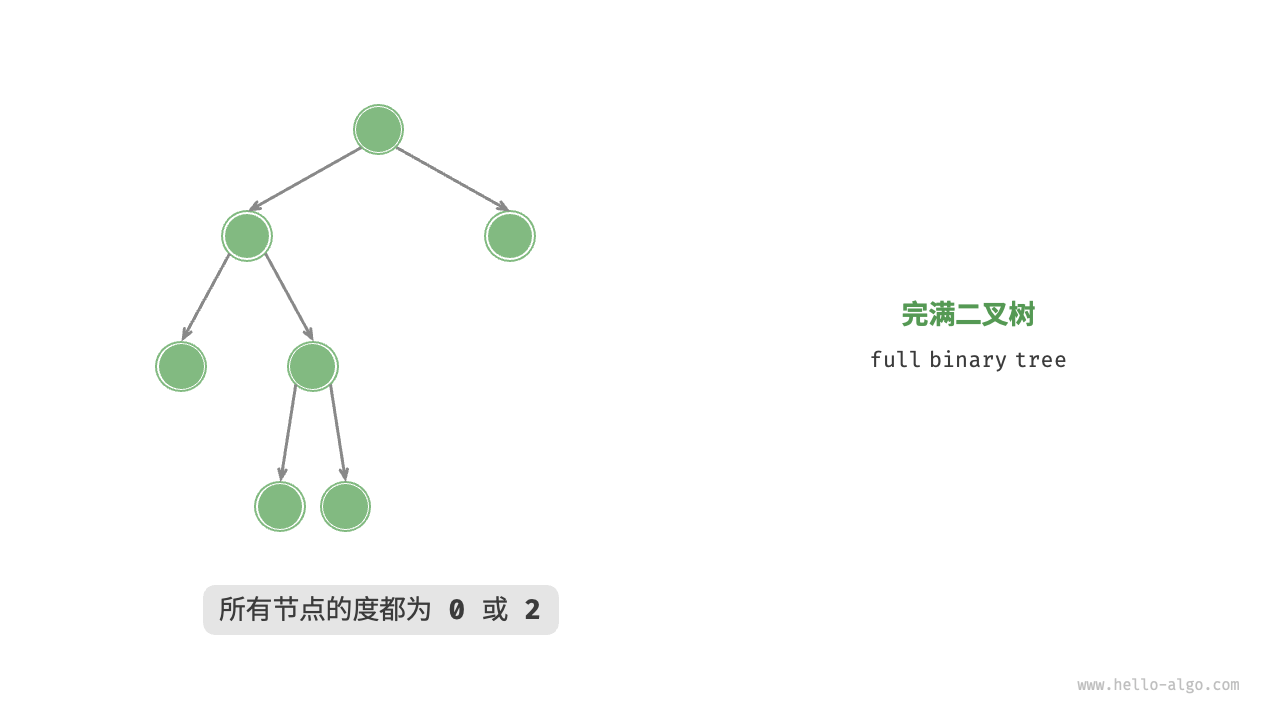
2.3 完满二叉树
满二叉树(full binary tree)除了叶节点之外,其余所有节点都有两个子节点。
2.4 平衡二叉树
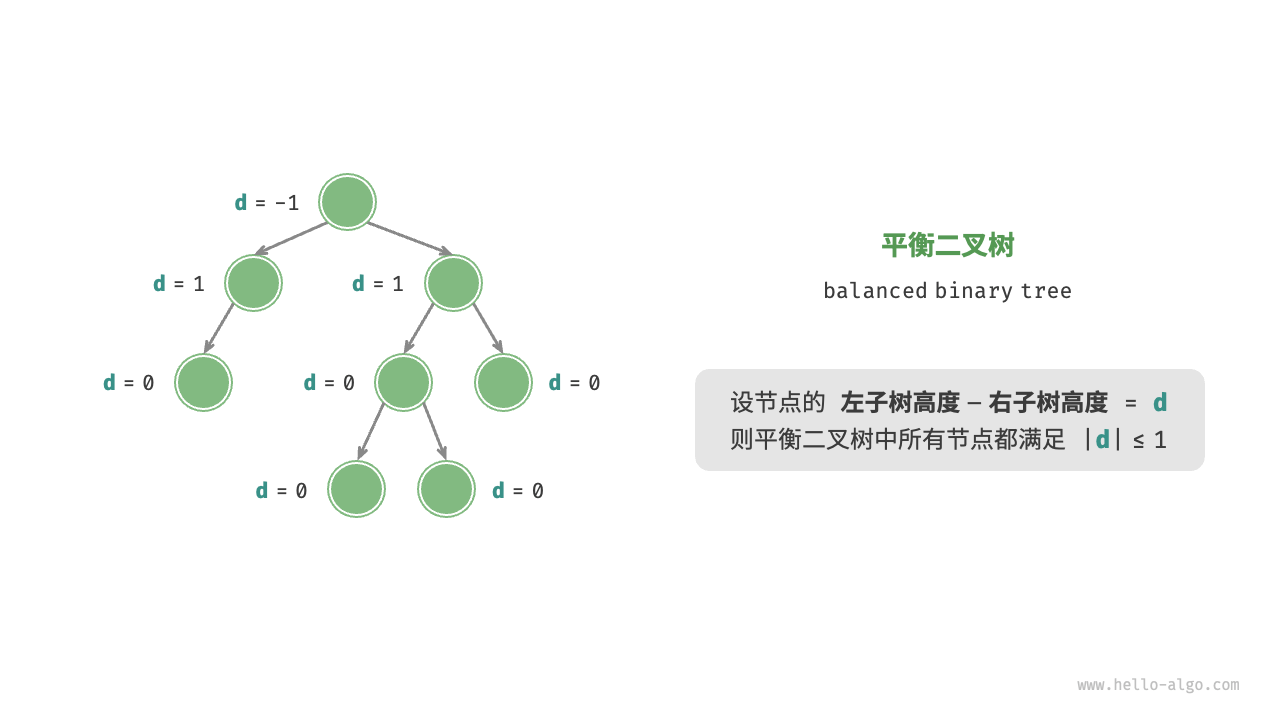
平衡二叉树(balanced binary tree)中任意节点的左子树和右子树的高度之差的绝对值不超过 1 。
3. 二叉树的遍历
3.1 层序遍历
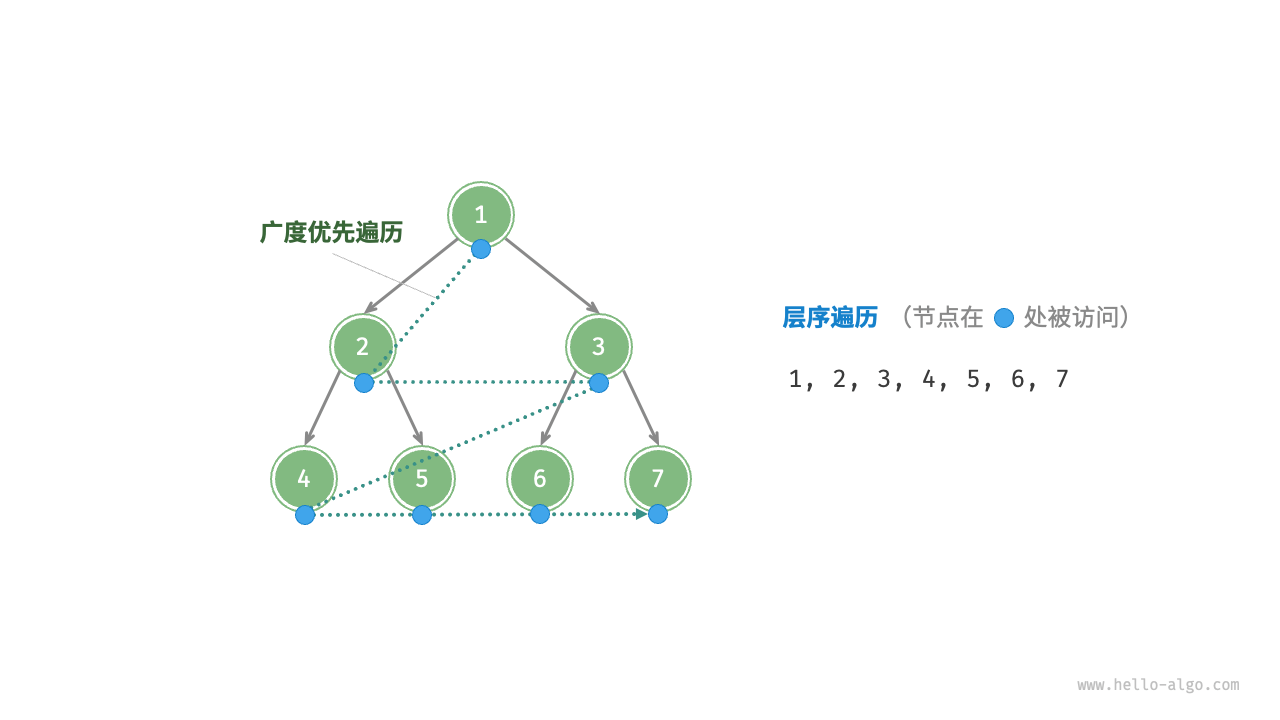
层序遍历(level-order traversal)从顶部到底部逐层遍历二叉树,并在每一层按照从左到右的顺序访问节点。
本质上属于广度优先遍历(breadth-first traversal),也称广度优先搜索(breadth-first search, BFS),体现了一种“一圈一圈向外扩展”的逐层遍历方式。
层序遍历代码实现:
使用队列的先进先出,来实现广度优先遍历
// 层序遍历
func levelOrder(root *TreeNode) []any {
// 初始化队列
queue := list.New()
queue.PushBack(root)
nums := make([]any, 0)
for queue.Len() > 0 {
// 队列出队
node := queue.Remove(queue.Front()).(*TreeNode)
nums = append(nums, node.Value)
// 如果左子节点不为nil,入队
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right != nil {
queue.PushBack(node.Right)
}
}
return nums
}测试
func TestNewTreeNode(t *testing.T) {
// 1.初始化节点
node1 := NewTreeNode(1)
node2 := NewTreeNode(2)
node3 := NewTreeNode(3)
node4 := NewTreeNode(4)
node5 := NewTreeNode(5)
node6 := NewTreeNode(6)
node7 := NewTreeNode(7)
// 2.构建二叉树
node1.Left = node2
node1.Right = node3
node2.Left = node4
node2.Right = node5
node3.Left = node6
node3.Right = node7
// 3.层序遍历二叉树
order := levelOrder(node1)
fmt.Println("层序遍历二叉树:", order)
}3.2 前,中,后序遍历
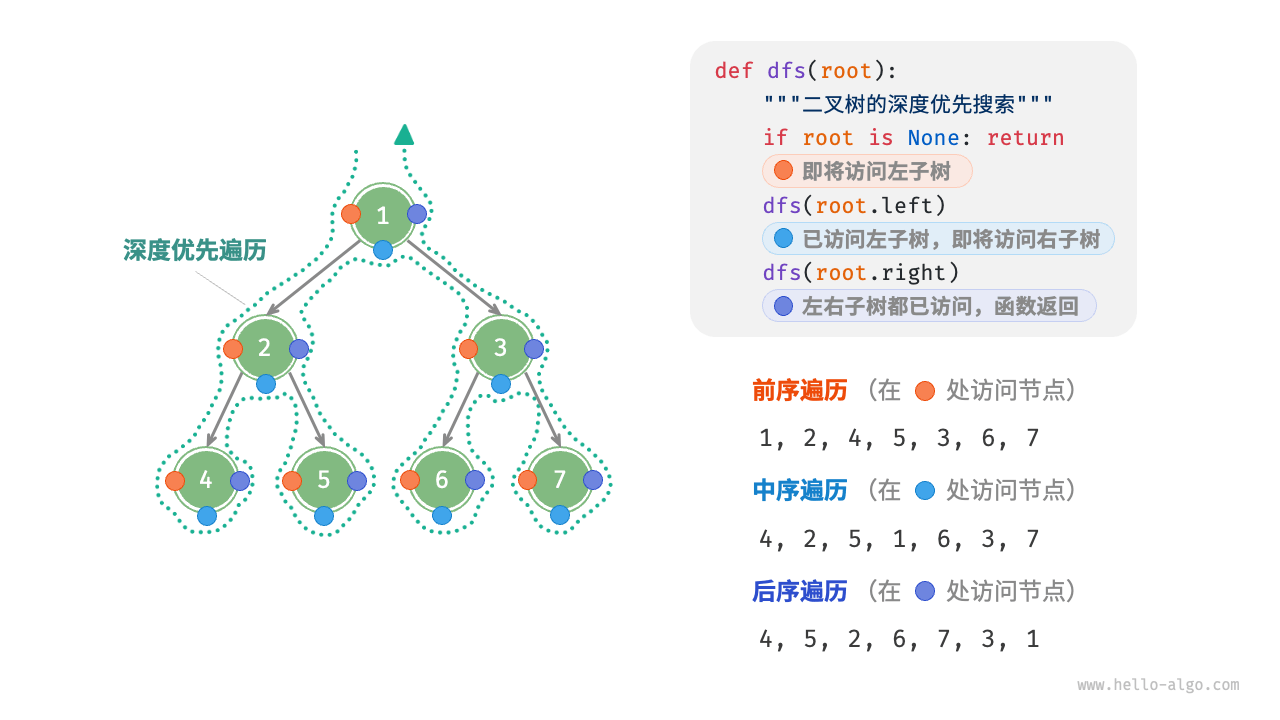
前,中,后序遍历代码实现
使用递归实现深度优先搜索
// 前序遍历
// 节点访问顺序 根 -> 左 -> 右
func PreOrder(node *TreeNode) []any {
var result []any
var preOrder func(node *TreeNode)
preOrder = func(node *TreeNode) {
if node == nil {
return
}
result = append(result, node.Value)
preOrder(node.Left)
preOrder(node.Right)
}
preOrder(node)
return result
}
// 中序遍历
// 节点访问顺序 左 -> 根 -> 右
func MiddleOrder(node *TreeNode) []any {
var result []any
var middleOrder func(node *TreeNode)
middleOrder = func(node *TreeNode) {
if node == nil {
return
}
middleOrder(node.Left)
result = append(result, node.Value)
middleOrder(node.Right)
}
middleOrder(node)
return result
}
// 后序遍历
// 节点访问顺序 左 -> 右 -> 根
func PostOrder(node *TreeNode) []any {
var result []any
var postOrder func(node *TreeNode)
postOrder = func(node *TreeNode) {
if node == nil {
return
}
postOrder(node.Left)
postOrder(node.Right)
result = append(result, node.Value)
}
postOrder(node)
return result
}测试
func TestNewTreeNode(t *testing.T) {
// 1.初始化节点
node1 := NewTreeNode(1)
node2 := NewTreeNode(2)
node3 := NewTreeNode(3)
node4 := NewTreeNode(4)
node5 := NewTreeNode(5)
node6 := NewTreeNode(6)
node7 := NewTreeNode(7)
// 2.构建二叉树
node1.Left = node2
node1.Right = node3
node2.Left = node4
node2.Right = node5
node3.Left = node6
node3.Right = node7
// 前序遍历
preOrderResult := PreOrder(node1)
fmt.Println("前序遍历:", preOrderResult)
// 中序遍历
middleOrderResult := MiddleOrder(node1)
fmt.Println("中序遍历:", middleOrderResult)
// 后序遍历
postOrderResult := PostOrder(node1)
fmt.Println("后序遍历:", postOrderResult)
}
4. 二叉树用数组表示
完美二叉树用数组表示
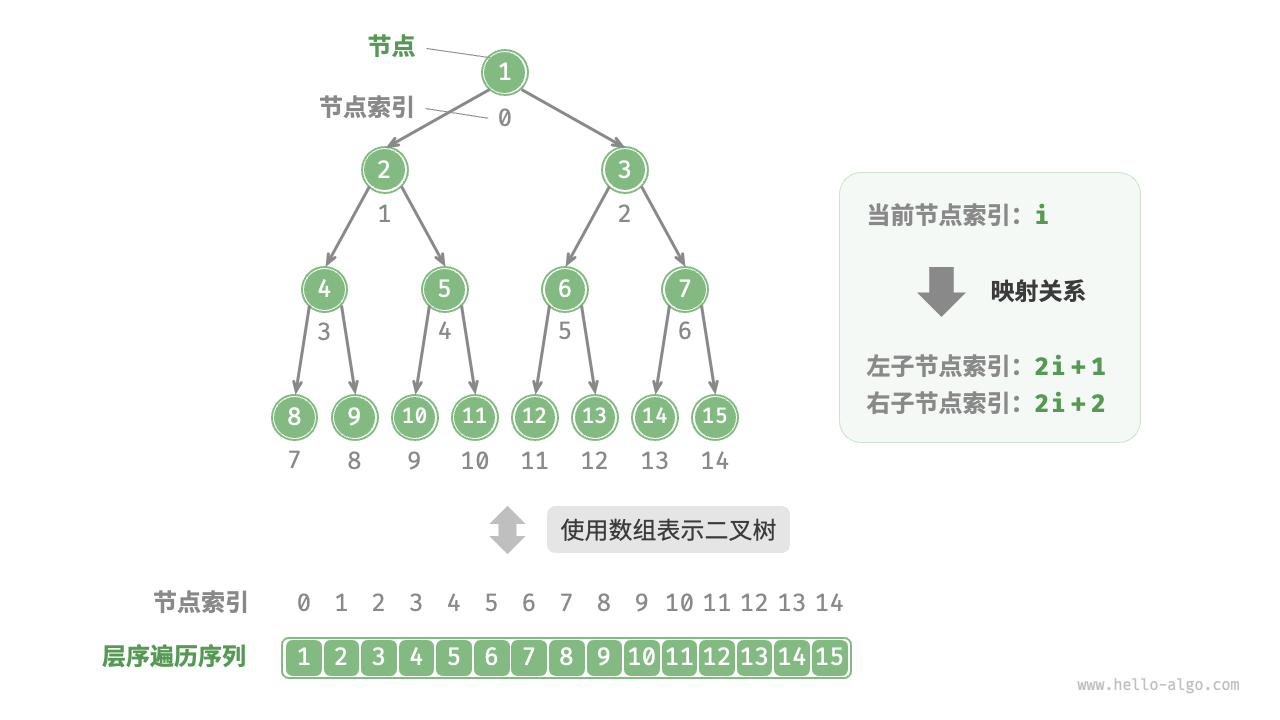
任意二叉树用数组表示
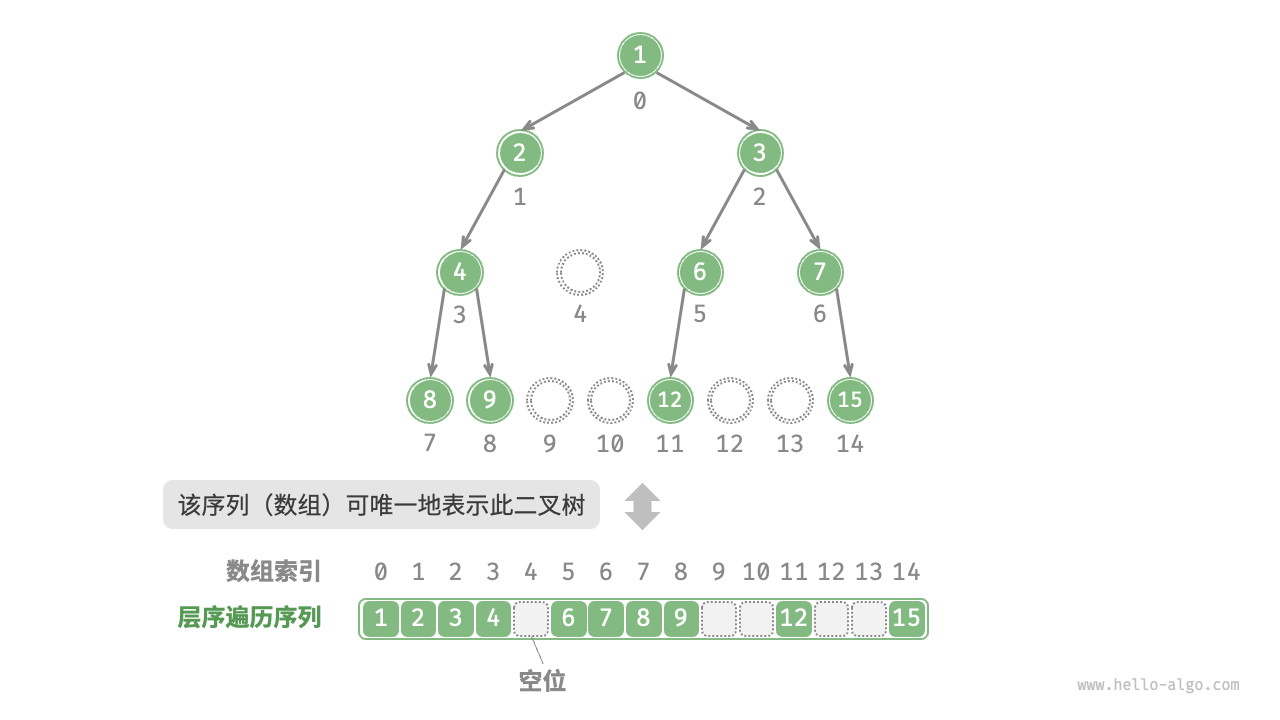
完全二叉树用数组表示
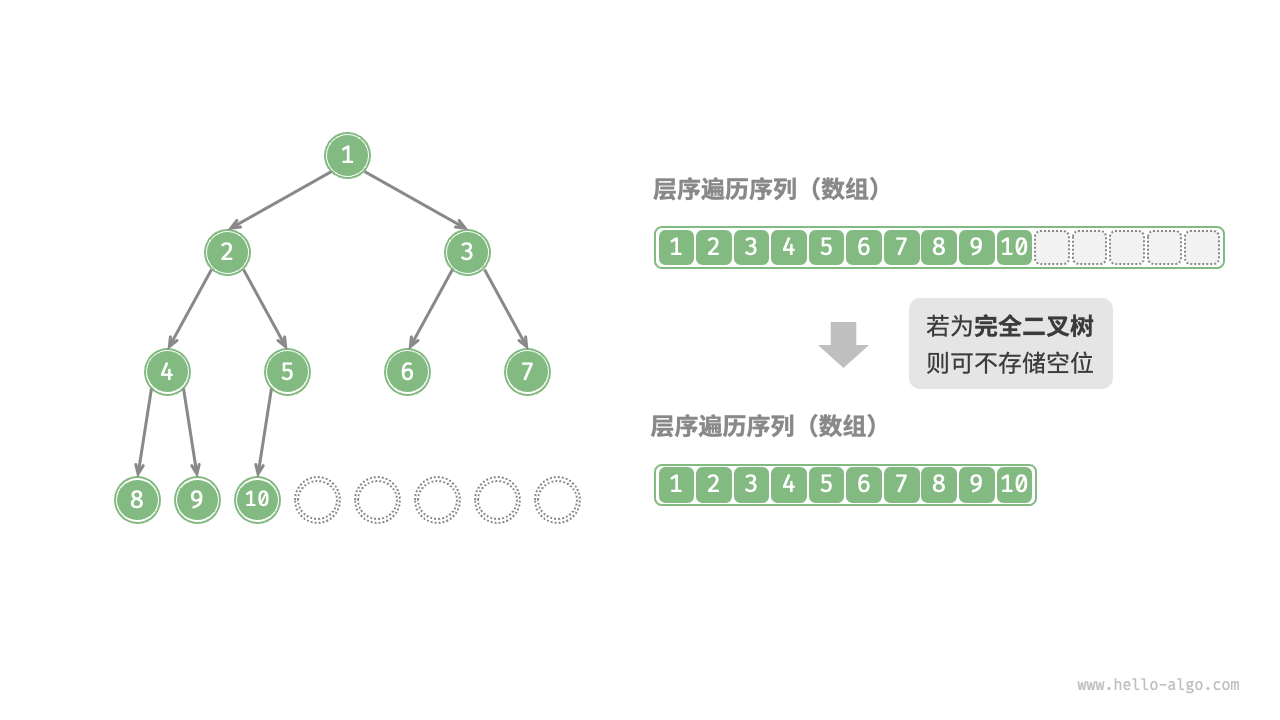
4.1 定义数组二叉树
// SliceBinaryTree 二叉树数组表示
type SliceBinaryTree struct {
// 因为表示任意二叉树需要有 nil,所以类型为 any
Tree []any
}
// NewSliceBinaryTree 构建数组二叉树
func NewSliceBinaryTree(tree []any) *SliceBinaryTree {
return &SliceBinaryTree{
Tree: tree,
}
}4.2 数组二叉树的基本操作
二叉树的数组表示主要有以下优点。
数组存储在连续的内存空间中,对缓存友好,访问与遍历速度较快。
不需要存储指针,比较节省空间。
允许随机访问节点。
然而,数组表示也存在一些局限性。
数组存储需要连续内存空间,因此不适合存储数据量过大的树。
增删节点需要通过数组插入与删除操作实现,效率较低。
当二叉树中存在大量
None时,数组中包含的节点数据比重较低,空间利用率较低。
5. 二叉搜索树
5.1 定义二叉搜索树
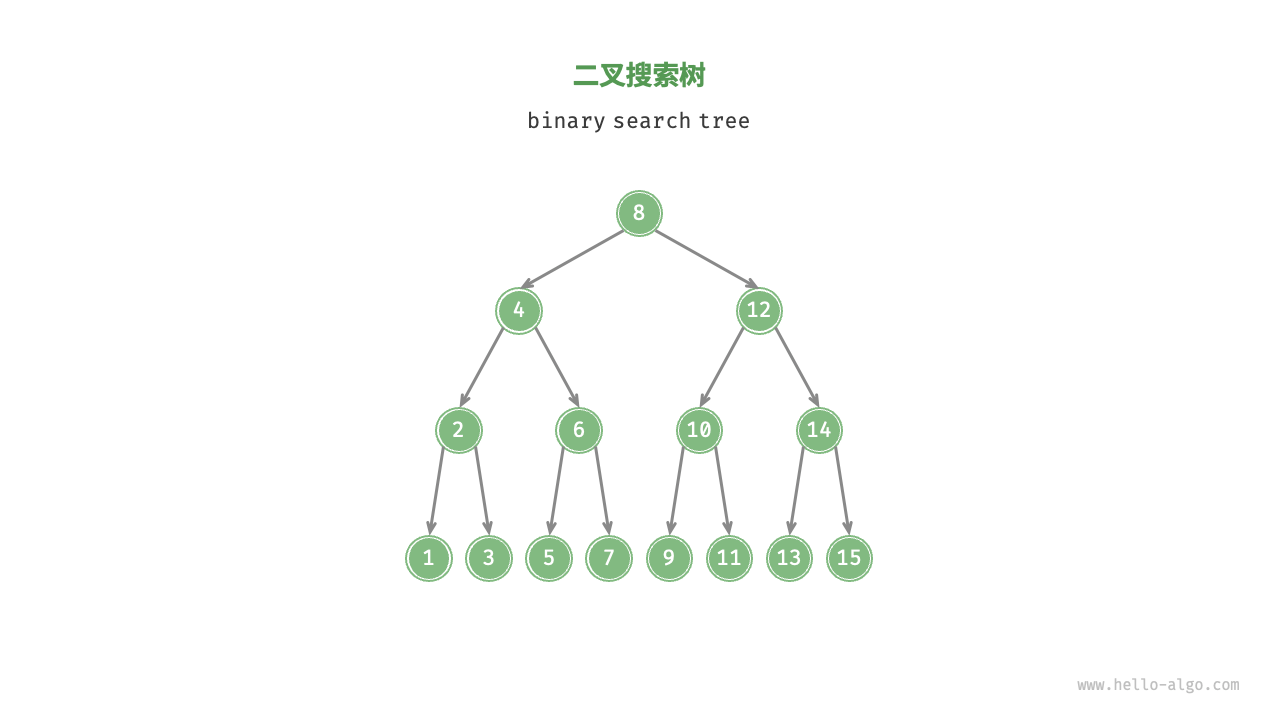
对于根节点,左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
任意节点的左、右子树也是二叉搜索树,即同样满足条件
1.。
// BinarySearchTree 定义二叉搜索树
type BinarySearchTree struct {
root *TreeNode
}
func NewBinarySearchTree() *BinarySearchTree {
return &BinarySearchTree{
root: nil,
}
}5.2 二叉搜索树的插入,删除,查找
代码实现
// InsertInto 插入
func (b *BinarySearchTree) InsertInto(value int) {
curNode := b.root
// 若树为空,初始化根节点
if curNode == nil {
b.root = NewTreeNode(value)
return
}
// 待插入节点之前的节点
var pre *TreeNode = nil
// 循环查找
for curNode != nil {
if curNode.Value == value {
return
}
if curNode.Value < value {
pre = curNode
curNode = curNode.Right
} else {
pre = curNode
curNode = curNode.Left
}
}
// 插入节点
node := NewTreeNode(value)
if pre.Value < value {
pre.Right = node
} else {
pre.Left = node
}
}
// 删除
// Search 查询
func (b *BinarySearchTree) Search(value int) *TreeNode {
curNode := b.root
for curNode != nil {
if curNode.Value < value {
curNode = curNode.Right
}
if curNode.Value > value {
curNode = curNode.Left
}
if curNode.Value == value {
return curNode
}
}
return nil
}测试
func TestNewBinarySearchTree(t *testing.T) {
// 初始化二叉树根节点
binarySearchTreeRoot := NewBinarySearchTree()
binarySearchTreeRoot.InsertInto(5)
binarySearchTreeRoot.InsertInto(2)
binarySearchTreeRoot.InsertInto(1)
binarySearchTreeRoot.InsertInto(7)
//
//fmt.Println(tree.root.Value)
//fmt.Println(tree.root.Left.Left.Value)
//fmt.Println(tree.root.Value)
//fmt.Println(tree.root.Right.Value)
}

评论区